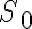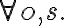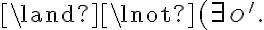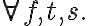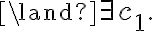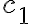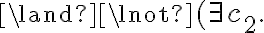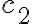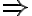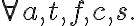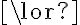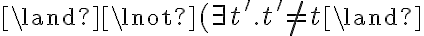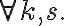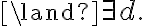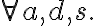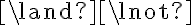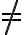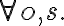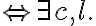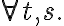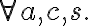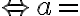Knowledge Representation & Reasoning
2. Logic-based knowledge representation and reasoning
2.3. Inferring a popcorn making plan
In this section, we introduce an axiomatization of the popcorn world, which allows us to derive a sequence of actions that achieves a subgoal of the popcorn making plan. We leave the specification of remaining axioms as an exercise to the reader. Let us consider the action sequence
- Put(Pot01, StoveCenter),
- Pour(Bowl01, Pot01),
- TurnKnob(switch(StoveCenter)),
- Wait(3),
- Put(Plate01, TableTopLeft),
- Pour(Pot01, Plate01).
We want to model actions and states in a way, such that a robot agent is able to automatically derive this action sequence as a plan that achieves its goal of having made popcorn in the kitchen environment and having served it on a plate. The initial state of the environment shall be
i.e., the unpopped corn is in the bowl on the right counter top, the cooking pot is in the right shelf, the plate in the left shelf, and the stove is switched off. Let the goal be that the corn has popped and is on a plate on one of the counter tops, i.e.,
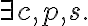 type(c, Corn)
type(c, Corn)  popped(c, s)
popped(c, s)  type(p, Plate)
type(p, Plate) 
In the previous section, we already provided a model of the Put action, which we can reuse so we move on and create a model of Pouring. The Pour(f,t) action denotes the transfer of a substance contained from a source container
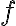 to a destination container
to a destination container 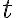 . For simplicity, we will assume here that any container can hold exactly one unit of volume, and that Pour will cause a complete transfer, i.e., there will not be any leftovers in the source container after pouring. As preconditions, we require the destination container to be empty and unobstructed. Unobstructed means that the container is not covered by anything (like a lid), and that there is sufficient free space above its opening such that the pouring can be performed. Obviously, in our popcorn world, a container is only unobstructed if it is located at one of the counter tops or the stove, and there is nothing on top of it, i.e.,
. For simplicity, we will assume here that any container can hold exactly one unit of volume, and that Pour will cause a complete transfer, i.e., there will not be any leftovers in the source container after pouring. As preconditions, we require the destination container to be empty and unobstructed. Unobstructed means that the container is not covered by anything (like a lid), and that there is sufficient free space above its opening such that the pouring can be performed. Obviously, in our popcorn world, a container is only unobstructed if it is located at one of the counter tops or the stove, and there is nothing on top of it, i.e.,We can now define the preconditions, under which pouring is possible, as
i.e., both 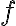 and
and 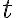 must be containers,
must be containers, 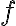 must be non-empty and accessible, and
must be non-empty and accessible, and 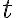 must be empty and unobstructed. As postconditions, Pour will cause the contents of the source container to be in the destination container, whereas it ceases being in the source container:
must be empty and unobstructed. As postconditions, Pour will cause the contents of the source container to be in the destination container, whereas it ceases being in the source container:
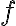 and
and 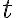 must be containers,
must be containers, 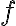 must be non-empty and accessible, and
must be non-empty and accessible, and 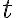 must be empty and unobstructed. As postconditions, Pour will cause the contents of the source container to be in the destination container, whereas it ceases being in the source container:
must be empty and unobstructed. As postconditions, Pour will cause the contents of the source container to be in the destination container, whereas it ceases being in the source container:The most interesting part of our popcorn example is the event when the corn pops. It is so interesting because it involves not only actions that transform the world state, but also physical and chemical processes that are captured in logical axioms. We will model the process in three parts: (1) the functionality of a switch, (2) the functionality of a stove, and (3) the popping process.
The core functionality of a switch is to toggle the state of an electrical device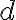 in a situation
in a situation  between switchedOn and
between switchedOn and 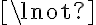 switchedOn. We introduce a TurnKnob(k) action, which operates on a knob and flips an electrical device's state. It is possible to execute TurnKnob(k) if
switchedOn. We introduce a TurnKnob(k) action, which operates on a knob and flips an electrical device's state. It is possible to execute TurnKnob(k) if 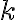 is a knob and belongs to an electrical device:
is a knob and belongs to an electrical device:
The core functionality of a switch is to toggle the state of an electrical device
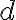 in a situation
in a situation  between switchedOn and
between switchedOn and 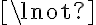 switchedOn. We introduce a TurnKnob(k) action, which operates on a knob and flips an electrical device's state. It is possible to execute TurnKnob(k) if
switchedOn. We introduce a TurnKnob(k) action, which operates on a knob and flips an electrical device's state. It is possible to execute TurnKnob(k) if 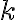 is a knob and belongs to an electrical device:
is a knob and belongs to an electrical device:where switch(d) is a function denoting the switch of an electrical device. TurnKnob(k) will change the state of the device it belongs to from 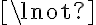 switchedOn(d,s) to switchedOn(d, do(TurnKnob(k),s)), and back:
switchedOn(d,s) to switchedOn(d, do(TurnKnob(k),s)), and back:
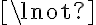 switchedOn(d,s) to switchedOn(d, do(TurnKnob(k),s)), and back:
switchedOn(d,s) to switchedOn(d, do(TurnKnob(k),s)), and back:When a stove is switched on, everything on its top will be exposed to heat. We can capture this introducing a fluent heated(o,s),
Note that in this formula, we have also modeled the heat conductivity of cooking pots, such that everything inside a pot will also be exposed to heat, when the pot is on a stove and the stove is switched on.
The final missing step in our world model is the popping process of the corn. In order for the corn to pop, it must be exposed to heat for 3 minutes. In a real-world setting, it would be desirable if a robot agent were able to spend the time until the corn has popped more useful, but for now we assume that it bridges this idle time with waiting. To this end, we introduce an action Wait(t), during which the agent sleeps for the given amount of time. First, let us specify that it is always possible to wait and do nothing:
The final missing step in our world model is the popping process of the corn. In order for the corn to pop, it must be exposed to heat for 3 minutes. In a real-world setting, it would be desirable if a robot agent were able to spend the time until the corn has popped more useful, but for now we assume that it bridges this idle time with waiting. To this end, we introduce an action Wait(t), during which the agent sleeps for the given amount of time. First, let us specify that it is always possible to wait and do nothing:
Time consuming processes like cooking or boiling can be elegantly modeled as postconditions of a waiting action, given that the world model satisfies certain conditions. In our example, we can state that the corn will have popped as a result of waiting for three minutes in a situation in which the corn is exposed to heat, i.e.,
Note that, in this case, there is no negative effect in the state successor axiom as the property of having popped is irreversible.
Starting from the initial state, it can be proven that our goal state in Equation can be reached by the action sequence
Starting from the initial state, it can be proven that our goal state in Equation can be reached by the action sequence
do(Pour(Pot01, Plate01),
do(Put(Plate01, TabletopLeft),
do(Wait(3)),
do(TurnKnob(switch(StoveCenter)),
do(Pour(Bowl01, Pot01),
Note that this solution is not unique. There are many alternative action sequences that achieve the goal state and many other ways of modelling the actions and processes one can think of. In kR&R, there is an entire subfield called qualitative physics and qualitative process theory that addresses this problem. A more thorough introduction to this field is beyond the scope of this chapter. We refer the interested reader to Brachman, Levesque 1985.