Knowledge Representation & Reasoning
2. Logic-based knowledge representation and reasoning
2.4. Complexity of logical reasoning
Representing models of the world and actions in situation calculus using FOL is extremely powerful and expressive, but comes with practical limitations. The perhaps most severe limitation affects the computational complexity of reasoning. Reasoning in logic denotes the automated verification of sentences given the facts and rules about the world. As an example, consider a rule, such as
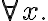 type(x, Bowl)
type(x, Bowl) 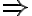 type(x, Container),
type(x, Container),
as part of a taxonomic relation stating that every object of the type bowl also is of the type container, and the fact type(Bowl01, Bowl) that assigns the entity Bowl01 the type Bowl. In order to prove that type(Bowl01, Container) also holds, we have to find a substitution of 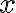 in the equation, such that the formula gets satisfied by its atomic constituents. This is the case for the substitution [x/Bowl01], as
in the equation, such that the formula gets satisfied by its atomic constituents. This is the case for the substitution [x/Bowl01], as
(type(x, Bowl) 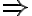 type(x, Container))[x/Bowl01]
type(x, Container))[x/Bowl01] type(Bowl01, Bowl)
type(Bowl01, Bowl) 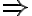 type(Bowl01, Container)
type(Bowl01, Container)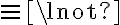 type(Bowl01, Bowl)
type(Bowl01, Bowl) 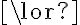 type(Bowl01, Container),
type(Bowl01, Container),
which is satisified if and only if type(Bowl01, Container) holds. The reasoning problem in FOL can thus be phrased as a search problem in the space of possible variable substitutions, which is called the Herbrandt universe. The elimination of variables by substitution through constant or function symbols is also called grounding or propositionalization, as a sentence whose variables have been substituted corresponds to an expression in propositional logic. However, the problem of finding a truth assignment satisfying a sentence in PL has been proven NP complete (Cook, 1971), so the computational expense of reasoning does scale exponentially in the number ground atoms. In addition, the Herbrandt universe typically is infinite as it contains both constant symbols and functions. As a consequence, it is not guaranteed that a search algorithm will terminate in all cases. It can be shown that every proposition that is entailed by a knowledge base in FOL can be deduced from a finite subset of the Herbrandt universe, whereas no method exists that is capable of proving non-entailment for all propositions that are not entailed by the knowledge base. This makes the reasoning problem in FOL semi-decidable (Turing, 1936; Church, 1936a; Church, 1936b). This means that for reasoning tasks that robots have to do it often pays off to limit the expressiveness of the representation language to what is needed and to think about whether the inference tasks can also be accomplished by more specific algorithms that can exploit the problem structure. Fast reasoning is particularly important for robot agents that are to act efficiently as in many cases the robot can start acting only after the reasoning tasks are completed.