Knowledge Representation & Reasoning
2. Logic-based knowledge representation and reasoning
We will now consider how the conceptualization of the popcorn making scenario that is described in Section 3 can be represented in order to infer sequences of robot actions that achieve the goals of the robot. To this end, we use the state space model of popcorn making as our running example. The problem of how to represent the necessary knowledge and reason with it is studied in the field of knowledge representation and reasoning (KR&R).
Shapiro, 2009 considers knowledge representation and reasoning as the study that is concerned with understanding, designing, and implementing ways of representing information in computers so that programs (agents) can use this information
- to derive information that is implied by it,
- to converse with people in natural language,
- to decide what to do next
- to plan future activities,
- to solve problems in areas that normally require human expertise.
McCarthy, 1968 identifies three fundamental features that an agent must support in order to make use of knowledge about the world:
- A set of explicit facts (Note, according to the terminology of logics we use the term fact, although in robotics the information robots use are often beliefs rather than facts that is that they cannot be guaranteed to be true) about the world that the agent already knows (or rather believes) to be true, including atomic propositions, rules, and equivalences, for instance.
- A TELL-interface that accepts new facts to be added to or removed from (1.)
- An ASK-interface that deduces new beliefs from that ones already existing in (1.).
Item (3.) refers to the capability of reasoning about aspects of the world, which denotes the use of representations of propositions in (1.) in order to derive new ones. In other words, the ability to reason allows to make propositions explicit that are implicitly entailed by the propositions already known.
Fig. 1: Knowledge representation hypothesis: "Any process capable of reasoning intelligently about the world must consist in part of a field of structures, of a roughly linguistic sort, which in some fashion represent whatever knowledge and beliefs the process may be said to possess." (Brachman, Levesque 1985)
The basic idea of the use of knowledge representation and reasoning for problem solving is visualized in Figure 1. A representation is a system of symbolic encodings of propositions that are believed to be true in the real world. Consequently, if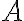 
represents 
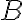, then 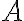is a placeholder for 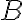and is usually more accessible than 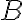. The mapping from a representational symbol to its counterpart in the real world is called its semantics. Our everyday life is full of symbols. We use 🍽️ for restaurant, ➕ for first aid, and we refer to people by their names when talking about them. Symbols do not only stand for things in the world, but can also be used to make general propositional statements. For example, 🚻➡️ stands for "the restrooms are on the right.''
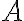represents 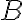, then 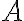is a placeholder for 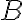and is usually more accessible than 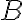. The mapping from a representational symbol to its counterpart in the real world is called its semantics. Our everyday life is full of symbols. We use 🍽️ for restaurant, ➕ for first aid, and we refer to people by their names when talking about them. Symbols do not only stand for things in the world, but can also be used to make general propositional statements. For example, 🚻➡️ stands for "the restrooms are on the right.''Representations are typically abstractions of entities and processes in the real-world. They are reduced to those aspects of the real world that are relevant for solving a particular category of problems. For our popcorn preparation setting, for instance, the groceries and kitchen items are task-relevant, whereas the song currently played on the radio is not relevant for most tasks.
Propositional rules specify how symbols relate to each other and can be used for reasoning. Reasoning denotes the process of manipulating the symbols in the representation to deduce a new representation. Such rules are also called sentences. For example, a rule like "IF perishable is true THEN in_refrigerator is true'' can be used for reasoning to draw the conclusion that in_refrigerator holds in the context underlying the model whenever perishable is believed to be true. (Note, the world may not comply with these axioms and there will always be inherent uncertainty in every 'true' statement.) The new deduced representation is then entailed by the original one. In an ideal situation, the propositions that are deduced from a representation match the aspects of the real world subject to their semantics.
Propositional rules specify how symbols relate to each other and can be used for reasoning. Reasoning denotes the process of manipulating the symbols in the representation to deduce a new representation. Such rules are also called sentences. For example, a rule like "IF perishable is true THEN in_refrigerator is true'' can be used for reasoning to draw the conclusion that in_refrigerator holds in the context underlying the model whenever perishable is believed to be true. (Note, the world may not comply with these axioms and there will always be inherent uncertainty in every 'true' statement.) The new deduced representation is then entailed by the original one. In an ideal situation, the propositions that are deduced from a representation match the aspects of the real world subject to their semantics.