Knowledge Representation & Reasoning
2. Logic-based knowledge representation and reasoning
2.1. Logic-based knowledge representation
We choose symbolic logic to formalize the entailment of conclusions from premises, in order to represent our model of popcorn making and robot agency in general. As shown in Figure 1, a logic formalism consists of three components: its syntax, its semantics, and its calculus:
- the syntax determines what can be expressed by defining the set of symbol structures that constitute the logic language. The language is typically defined recursively through a set of atomic symbols and grammatical rules that define how symbolic expressions in the language can be combined to form more complex structures
- the semantics determines what symbolic expressions mean by assigning the truth value to symbolic expression, where the semantics of atomic expressions is specified by an interpretation function and the semantics of a compound expression is computed from its constituents and the logical operator that connects the the constituents such as the "and,'' "or,'' and "negation'' operator.
- the calculus that consists of symbolic expressions asserted to be true and rules for generating new symbol expressions from existing ones.
Fig. 1: Components of a logic knowledge representation: syntax, semantics, and calculus.
If we use logic to encode problem-solving knowledge then the calculus of a logic can operate as a problem-solver. To this end, knowledge engineers have to carefully define the semantics of the atomic expressions. In addition, the the engineer has to assert a set of compound symbolic expressions as being true. The goal is to determine a compact set of expressions (an axiomatization) that together with the rules of the calculus creates only symbol structures that are entailed by the semantics, it is that the axiomatization is correct and that all symbolic expressions that are entailed can be generated by applying the calculus to the axiomatization, that is that the axiomatization is complete. Thus, if the knowledge engineer comes up with a correct and complete axiomatization of a problem domain, then a symbolic expression that represents some proposition in this domain is true if and only if it can be derived from the axiomatization using the calculus. This is important because this gives us an automatable computation process to test the truth of a symbolic expression.
Propositional logic. Let us consider propositional logic (PL) as our first example of a logic. In PL, every symbol is a Boolean proposition that can take the values true or false. A symbol thus is an atomic sentence, which cannot be further decomposed into finer-grained sentences. Two sentences may be connected by means of logical connectives  ('and'),
('and'), 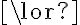 ('or'),
('or'), 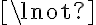 ('not'),
('not'), 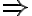 ('implies') and
('implies') and 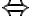 ('equivalent') to form more complex sentences (in descending operator precedence). Brackets
('equivalent') to form more complex sentences (in descending operator precedence). Brackets 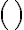 may be used to accommodate precedence of connectives. In PL, we can represent the knowledge that the corn will pop when it is in the pot, the pot is located on the stove and the stove is switched on as follows:
may be used to accommodate precedence of connectives. In PL, we can represent the knowledge that the corn will pop when it is in the pot, the pot is located on the stove and the stove is switched on as follows:
corn-in-pot  pot-on-stove
pot-on-stove  stove-switched-on
stove-switched-on 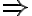 corn-popped
corn-popped
The semantics of this representation of an implication is that, whenever we encounter the antecedant of both corn-in-pot, pot-on-stove, and stove-switched-on to be true, we can be sure that corn-popped will also be true. Starting from those three antecedant expressions, a calculus of PL should thus be able to derive corn-popped as a new expression.
PL is simple and intuitive, but at the same time limited in expressiveness and generality. What this means becomes evident if we try to apply the above representation to a kitchen with more than one stove tops, let us assume four. In order to represent the same knowledge, in the new environment we would need four sentences, one for every stove top, i.e.
corn-in-pot  pot-on-stove1
pot-on-stove1  stove-1-switched-on
stove-1-switched-on 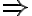 corn-popped
corn-popped
corn-in-pot  pot-on-stove2
pot-on-stove2  stove-2-switched-on
stove-2-switched-on 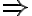 corn-popped
corn-popped
corn-in-pot  pot-on-stove3
pot-on-stove3  stove-3-switched-on
stove-3-switched-on 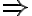 corn-popped
corn-popped
corn-in-pot  pot-on-stove4
pot-on-stove4  stove-4-switched-on
stove-4-switched-on 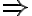 corn-popped
corn-popped
 , Kilogram, or X. Propositions are made by means of predicates that are used to establish certain relations between symbols. For example, a binary in predicate can be used to establish a relation between the symbols for the corn and the cooking pot:
, Kilogram, or X. Propositions are made by means of predicates that are used to establish certain relations between symbols. For example, a binary in predicate can be used to establish a relation between the symbols for the corn and the cooking pot: connectives to form more complex expressions, such as
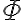 containing a universally quantified variable
containing a universally quantified variable 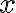 is written as
is written as 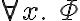 , (literally "for all x'') and a sentence
, (literally "for all x'') and a sentence 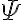 containing an existentially quantified variable is written
containing an existentially quantified variable is written 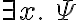 (literally, "there exists x''). Consequently, using the universal quantifier
(literally, "there exists x''). Consequently, using the universal quantifier 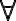 , we can represent the knowledge that in general, corn pops when it is put in a cooking pot, which is located on a stove and the stove is turned on:
, we can represent the knowledge that in general, corn pops when it is put in a cooking pot, which is located on a stove and the stove is turned on: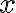 is being substituted by the symbol
is being substituted by the symbol 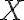 in a sentence
in a sentence 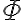 , we write
, we write ![\Phi[x/X] \Phi[x/X]](https://intel4coro.informatik.uni-bremen.de/filter/tex/pix.php/9254e54e7ed508ab438383e6dd5e362f.gif) .
.Besides constant and predicate symbols, a third kind of symbols are functions. The term 'function', in context of FOL, however, does not refer to a kind of sub-routine that takes arguments and returns a value. It is rather to be understood as an elegant way of referring to related things without the need of introducting a symbol for them. For example, we naturally talk about "the location of the corn'' without explicitly mentioning what the actual location is. The label "location of the corn'' always refers to the correct thing, even if we do not know what it is. Functions in FOL give us the same flexibility in computational knowledge representation. The function
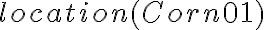 , for instance, is a way of denoting the location of the corn in every possible state of the environment without knowing about its actual location. A function is a valid representational symbol itself, so functions can also be nested.
, for instance, is a way of denoting the location of the corn in every possible state of the environment without knowing about its actual location. A function is a valid representational symbol itself, so functions can also be nested. 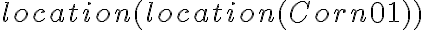 , for example, denotes the location of the corn's location. As functions are representational terms, however, they are not valid sentences. Valid sentences about functions can be made through predicates, just like ordinary constant symbols, or by making their identity explicit using the equality operator '
, for example, denotes the location of the corn's location. As functions are representational terms, however, they are not valid sentences. Valid sentences about functions can be made through predicates, just like ordinary constant symbols, or by making their identity explicit using the equality operator ' '. At this point it is important to note that the semantics of a FOL is typically non-injective and non-surjective. This means that the mapping from symbols to objects in the real world is not necessarily complete and unambiguous, such that there may be objects that are not represented by any symbol, and there may be objects referred to by more than one symbol. The fact that two symbols refer to the identical object can be stated with the equality operator. In our running example, for instance,
'. At this point it is important to note that the semantics of a FOL is typically non-injective and non-surjective. This means that the mapping from symbols to objects in the real world is not necessarily complete and unambiguous, such that there may be objects that are not represented by any symbol, and there may be objects referred to by more than one symbol. The fact that two symbols refer to the identical object can be stated with the equality operator. In our running example, for instance,