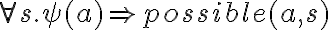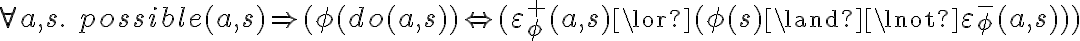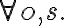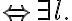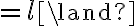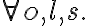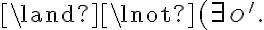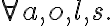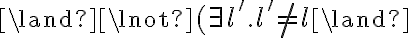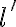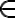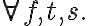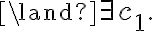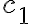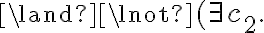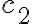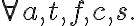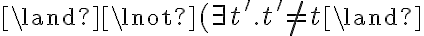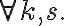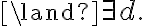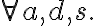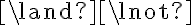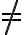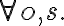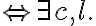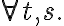Knowledge Representation & Reasoning
| Site: | Integrated E-Learning 4 Cognitive Robotics |
| Course: | Knowledge Representation & Reasoning |
| Book: | Knowledge Representation & Reasoning |
| Printed by: | Guest user |
| Date: | Friday, February 6, 2026, 7:00 AM |
1. Knowledge-enabled agent architecture
Let us now turn to the issue of how to realize the agent function. In its simplest form, we can realize the agent function as a function that maps a percept and directly map to the action to be executed next. This kind of realizing the agent function is called a reflex agent, which is often implemented in the form of simple if-then rules of the form "if you bump into an obstacle, turn around by 90 degrees.''
For robot agents that are to accomplish more complex tasks, a purely reactive action selection strategy is not sufficient. This holds for several reasons including that often environments are only partially observable, such that the best decision cannot be made on the current percept only. For example, consider the objects in a closed drawer, which the robot should remember after it has detected them. An effective approach to dealing with partial observability is to maintain an internal representation of the state of the environment, which is updated according to the percepts in every iteration of the perception action loop. For example, the state of the environment can include spatial relations of objects (e.g., locations and containers, etc.) as well as their internal state (e.g., switched on, fill level, etc.). We call this internal representation of the environment a model of the environment or a world model.
In many cases, the performance of the agent function can be further improved if the agent takes, in addition, its experiences and expectations into account. For complex tasks such as meal preparation, the action selection can be informed not only by the state of the environment but also based on the experience collected from former actions and the expectations about the effects of future actions. For example, in order to pick up an object from a drawer, the drawer must be opened first to make the objects inside accessible in the case that it is closed. In order to place an object at a specific location, it must be grasped with the agent's gripper first and in order to grasp an object, the gripper must be opened and must not already hold a different object. In order to take the right decisions, the agent thus must also have a model of its actions and their effects in the environment and which conditions the environment must be fulfilled for an action to be applicable. We refer to the specification of an action's effects and their applicability as an action's pre and post conditions. The preconditions represent conditions under which an action is executable and the postconditions specify the effects that the execution of an action has in the environment.
Fig. 1: Schema of a knowledge-enabled implementation of the rational agent function: The sequence of percepts is first interpreted by a perception component of the agent to get an updated formal representation of the world model. Based on the agent's actions and the world state, all possible action sequences are enumerated. By projecting forward the effects of each action in the sequence, a final state is obtained. If the final state satisfies the agent's goals, a plan for achieving a goal has been found, which is returned as a solution.
We consider a knowledge-enabled robot agent to be a robot agent that is equipped with symbolic representations of the rational robot agent model. An advantage of knowledge-enabled robot agents over reactive agents is that they can infer action sequences that are predicted to achieve a given goal. In this setting, the goal is being specified as the set of environment states that satisfy the given goal. For example, a possible goal specification of a popcorn preparation task is "the corn has popped and is located in a bowl. All devices are switched off.''
A possible realization of the process of inferring a goal-achieving action sequence a knowledge-enabled agent function is visualized in Figure 3. The action sequence generator enumerates all possible sequences of actions that the robot agent can perform, starting from the initial state of the environment model. By successively applying the pre- and postconditions of all actions in a sequence, the environment models' final state after execution of the whole sequence is obtained. If the resulting state satisfies a goal state, the agent function has found a solution and the respective action sequence is returned for execution. We call such an action sequence a robot action plan. If the goal state is not satisfied in the resulting environment state, the next action sequence from the action sequence generator is examined. The process of finding a sequence of actions that achieves goal states is called the planning problem.
2. Logic-based knowledge representation and reasoning
We will now consider how the conceptualization of the popcorn making scenario that is described in Section 3 can be represented in order to infer sequences of robot actions that achieve the goals of the robot. To this end, we use the state space model of popcorn making as our running example. The problem of how to represent the necessary knowledge and reason with it is studied in the field of knowledge representation and reasoning (KR&R).
Shapiro, 2009 considers knowledge representation and reasoning as the study that is concerned with understanding, designing, and implementing ways of representing information in computers so that programs (agents) can use this information
- to derive information that is implied by it,
- to converse with people in natural language,
- to decide what to do next
- to plan future activities,
- to solve problems in areas that normally require human expertise.
- A set of explicit facts (Note, according to the terminology of logics we use the term fact, although in robotics the information robots use are often beliefs rather than facts that is that they cannot be guaranteed to be true) about the world that the agent already knows (or rather believes) to be true, including atomic propositions, rules, and equivalences, for instance.
- A TELL-interface that accepts new facts to be added to or removed from (1.)
- An ASK-interface that deduces new beliefs from that ones already existing in (1.).
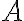 represents
represents 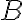 , then
, then 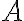 is a placeholder for
is a placeholder for 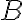 and is usually more accessible than
and is usually more accessible than 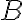 . The mapping from a representational symbol to its counterpart in the real world is called its semantics. Our everyday life is full of symbols. We use 🍽️ for restaurant, ➕ for first aid, and we refer to people by their names when talking about them. Symbols do not only stand for things in the world, but can also be used to make general propositional statements. For example, 🚻➡️ stands for "the restrooms are on the right.''
. The mapping from a representational symbol to its counterpart in the real world is called its semantics. Our everyday life is full of symbols. We use 🍽️ for restaurant, ➕ for first aid, and we refer to people by their names when talking about them. Symbols do not only stand for things in the world, but can also be used to make general propositional statements. For example, 🚻➡️ stands for "the restrooms are on the right.''Propositional rules specify how symbols relate to each other and can be used for reasoning. Reasoning denotes the process of manipulating the symbols in the representation to deduce a new representation. Such rules are also called sentences. For example, a rule like "IF perishable is true THEN in_refrigerator is true'' can be used for reasoning to draw the conclusion that in_refrigerator holds in the context underlying the model whenever perishable is believed to be true. (Note, the world may not comply with these axioms and there will always be inherent uncertainty in every 'true' statement.) The new deduced representation is then entailed by the original one. In an ideal situation, the propositions that are deduced from a representation match the aspects of the real world subject to their semantics.
2.1. Logic-based knowledge representation
We choose symbolic logic to formalize the entailment of conclusions from premises, in order to represent our model of popcorn making and robot agency in general. As shown in Figure 1, a logic formalism consists of three components: its syntax, its semantics, and its calculus:
- the syntax determines what can be expressed by defining the set of symbol structures that constitute the logic language. The language is typically defined recursively through a set of atomic symbols and grammatical rules that define how symbolic expressions in the language can be combined to form more complex structures
- the semantics determines what symbolic expressions mean by assigning the truth value to symbolic expression, where the semantics of atomic expressions is specified by an interpretation function and the semantics of a compound expression is computed from its constituents and the logical operator that connects the the constituents such as the "and,'' "or,'' and "negation'' operator.
- the calculus that consists of symbolic expressions asserted to be true and rules for generating new symbol expressions from existing ones.
Fig. 1: Components of a logic knowledge representation: syntax, semantics, and calculus.
If we use logic to encode problem-solving knowledge then the calculus of a logic can operate as a problem-solver. To this end, knowledge engineers have to carefully define the semantics of the atomic expressions. In addition, the the engineer has to assert a set of compound symbolic expressions as being true. The goal is to determine a compact set of expressions (an axiomatization) that together with the rules of the calculus creates only symbol structures that are entailed by the semantics, it is that the axiomatization is correct and that all symbolic expressions that are entailed can be generated by applying the calculus to the axiomatization, that is that the axiomatization is complete. Thus, if the knowledge engineer comes up with a correct and complete axiomatization of a problem domain, then a symbolic expression that represents some proposition in this domain is true if and only if it can be derived from the axiomatization using the calculus. This is important because this gives us an automatable computation process to test the truth of a symbolic expression.
Propositional logic. Let us consider propositional logic (PL) as our first example of a logic. In PL, every symbol is a Boolean proposition that can take the values true or false. A symbol thus is an atomic sentence, which cannot be further decomposed into finer-grained sentences. Two sentences may be connected by means of logical connectives  ('and'),
('and'), 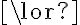 ('or'),
('or'), 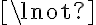 ('not'),
('not'), 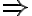 ('implies') and
('implies') and 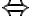 ('equivalent') to form more complex sentences (in descending operator precedence). Brackets
('equivalent') to form more complex sentences (in descending operator precedence). Brackets 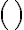 may be used to accommodate precedence of connectives. In PL, we can represent the knowledge that the corn will pop when it is in the pot, the pot is located on the stove and the stove is switched on as follows:
may be used to accommodate precedence of connectives. In PL, we can represent the knowledge that the corn will pop when it is in the pot, the pot is located on the stove and the stove is switched on as follows:
corn-in-pot  pot-on-stove
pot-on-stove  stove-switched-on
stove-switched-on 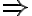 corn-popped
corn-popped
The semantics of this representation of an implication is that, whenever we encounter the antecedant of both corn-in-pot, pot-on-stove, and stove-switched-on to be true, we can be sure that corn-popped will also be true. Starting from those three antecedant expressions, a calculus of PL should thus be able to derive corn-popped as a new expression.
PL is simple and intuitive, but at the same time limited in expressiveness and generality. What this means becomes evident if we try to apply the above representation to a kitchen with more than one stove tops, let us assume four. In order to represent the same knowledge, in the new environment we would need four sentences, one for every stove top, i.e.
corn-in-pot  pot-on-stove1
pot-on-stove1  stove-1-switched-on
stove-1-switched-on 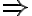 corn-popped
corn-popped
corn-in-pot  pot-on-stove2
pot-on-stove2  stove-2-switched-on
stove-2-switched-on 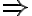 corn-popped
corn-popped
corn-in-pot  pot-on-stove3
pot-on-stove3  stove-3-switched-on
stove-3-switched-on 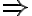 corn-popped
corn-popped
corn-in-pot  pot-on-stove4
pot-on-stove4  stove-4-switched-on
stove-4-switched-on 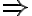 corn-popped
corn-popped
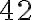 , Kilogram, or X. Propositions are made by means of predicates that are used to establish certain relations between symbols. For example, a binary in predicate can be used to establish a relation between the symbols for the corn and the cooking pot:
, Kilogram, or X. Propositions are made by means of predicates that are used to establish certain relations between symbols. For example, a binary in predicate can be used to establish a relation between the symbols for the corn and the cooking pot: connectives to form more complex expressions, such as
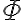 containing a universally quantified variable
containing a universally quantified variable 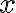 is written as
is written as 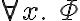 , (literally "for all x'') and a sentence
, (literally "for all x'') and a sentence 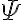 containing an existentially quantified variable is written
containing an existentially quantified variable is written 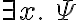 (literally, "there exists x''). Consequently, using the universal quantifier
(literally, "there exists x''). Consequently, using the universal quantifier 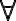 , we can represent the knowledge that in general, corn pops when it is put in a cooking pot, which is located on a stove and the stove is turned on:
, we can represent the knowledge that in general, corn pops when it is put in a cooking pot, which is located on a stove and the stove is turned on: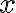 is being substituted by the symbol
is being substituted by the symbol 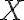 in a sentence
in a sentence 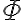 , we write
, we write ![\Phi[x/X] \Phi[x/X]](https://intel4coro.informatik.uni-bremen.de/filter/tex/pix.php/9254e54e7ed508ab438383e6dd5e362f.gif) .
.Besides constant and predicate symbols, a third kind of symbols are functions. The term 'function', in context of FOL, however, does not refer to a kind of sub-routine that takes arguments and returns a value. It is rather to be understood as an elegant way of referring to related things without the need of introducting a symbol for them. For example, we naturally talk about "the location of the corn'' without explicitly mentioning what the actual location is. The label "location of the corn'' always refers to the correct thing, even if we do not know what it is. Functions in FOL give us the same flexibility in computational knowledge representation. The function
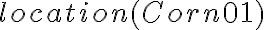 , for instance, is a way of denoting the location of the corn in every possible state of the environment without knowing about its actual location. A function is a valid representational symbol itself, so functions can also be nested.
, for instance, is a way of denoting the location of the corn in every possible state of the environment without knowing about its actual location. A function is a valid representational symbol itself, so functions can also be nested. 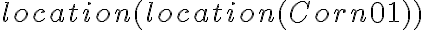 , for example, denotes the location of the corn's location. As functions are representational terms, however, they are not valid sentences. Valid sentences about functions can be made through predicates, just like ordinary constant symbols, or by making their identity explicit using the equality operator '
, for example, denotes the location of the corn's location. As functions are representational terms, however, they are not valid sentences. Valid sentences about functions can be made through predicates, just like ordinary constant symbols, or by making their identity explicit using the equality operator ' '. At this point it is important to note that the semantics of a FOL is typically non-injective and non-surjective. This means that the mapping from symbols to objects in the real world is not necessarily complete and unambiguous, such that there may be objects that are not represented by any symbol, and there may be objects referred to by more than one symbol. The fact that two symbols refer to the identical object can be stated with the equality operator. In our running example, for instance,
'. At this point it is important to note that the semantics of a FOL is typically non-injective and non-surjective. This means that the mapping from symbols to objects in the real world is not necessarily complete and unambiguous, such that there may be objects that are not represented by any symbol, and there may be objects referred to by more than one symbol. The fact that two symbols refer to the identical object can be stated with the equality operator. In our running example, for instance, 2.2. Logic-based action planning
In order to model the evolution of the world over time, we describe a
framework in FOL called situation calculus. In situation calculus, world states and actions' pre- and postconditions are bound to an abstract symbol representing a certain situation. In context of a robot agent, a situation represents one cycle in the perception-action loop:
- Technically, a situation is denoted by a term in FOL, i.e., the constant symbol
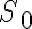 denoting the initial situation, or a function
denoting the initial situation, or a function 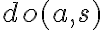 representing the situation that is obtained when an action
representing the situation that is obtained when an action  is executed in situation
is executed in situation  .
. - Actions are represented by terms in FOL. Constant symbols stand for actions without arguments (e.g., Stop), and functions represent actions that can be parameterized (e.g., Open(DrawerLeft)). There is a dedicated predicate
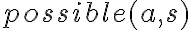 , which states that an action
, which states that an action  is applicable in situation
is applicable in situation  .
. - Fluents represent certain aspects of a world state that may change from one situation to another. Fluents can be represented by predicates, like
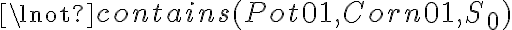 or functions like
or functions like 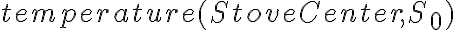 ). Fluents are always bound to specific situations that they refer to because they may change their values over time. States that are constant over all situations are called atemporary and do not need to be assigned a situation. Examples of such predicates are the \textit{type} assertions as introduced above, such as
). Fluents are always bound to specific situations that they refer to because they may change their values over time. States that are constant over all situations are called atemporary and do not need to be assigned a situation. Examples of such predicates are the \textit{type} assertions as introduced above, such as 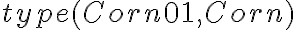 .
.
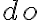 is also called projection as it predicts the states of future situations that are obtained through action execution. By nesting multiple do functions, one can represent the final situation that is obtained after execution of a complete sequence of actions. For example, the situation after execution of the three actions
is also called projection as it predicts the states of future situations that are obtained through action execution. By nesting multiple do functions, one can represent the final situation that is obtained after execution of a complete sequence of actions. For example, the situation after execution of the three actions- Put(Pot01, StoveCenter)
- Pour(Bowl01, Pot01)
- TurnKnow(switch(StoveCenter))
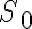 through fluent and atemporal axioms. In order to describe the popcorn world, for instance, we have to assert the types of objects in our environment:
through fluent and atemporal axioms. In order to describe the popcorn world, for instance, we have to assert the types of objects in our environment: type(ShelfLeft, Shelf)
type(ShelfLeft, Shelf)  type(ShelfRight, Shelf)
type(ShelfRight, Shelf) type(Corn01, Corn)
type(Corn01, Corn)  type(Pot01, CookingPot)
type(Pot01, CookingPot) type(Bowl01, Bowl)
type(Bowl01, Bowl)  type(Plate01, Plate)
type(Plate01, Plate)Action axioms. Actions are represented by two kinds of axioms, the possibility axiom}, which specifies under which circumstances an action is possible, and a successor state axiom, which describes the way in which the successor situation is affected by an action. The possibility axioms are sentences in FOL of the form
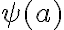 is a sentence with a free variable
is a sentence with a free variable  specifying the preconditions of the action
specifying the preconditions of the action 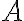 . The successor states are specified by axioms of the form
. The successor states are specified by axioms of the form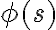 is a fluent declaration in situation
is a fluent declaration in situation  and
and 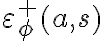 is a specification of the positive effects of an action
is a specification of the positive effects of an action  on
on 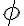 in situation
in situation  . Analogously,
. Analogously, 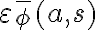 specifies the negative effects of action
specifies the negative effects of action  on
on 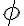 in
in  . An axiom of the form of the Equation can be read as follows: "In a situation
. An axiom of the form of the Equation can be read as follows: "In a situation  where action
where action  is applicable, the fluent
is applicable, the fluent 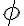 will hold after execution of
will hold after execution of  if and only if
if and only if  has made
has made 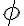 true (positive effect), or
true (positive effect), or 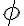 was already true in
was already true in  and
and  did not make
did not make 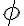 false (negative effect).''
false (negative effect).''change is not enough. In most cases, only a small subset of fluents will be affected by an action and nearly all others stay the same. In FOL, this needs to be explicitly stated. In order to account for this problem, which is also known as the frame problem, it is necessary to also consider
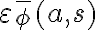 in the successor state axiom.
in the successor state axiom.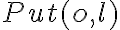 , which denotes the action of putting an object
, which denotes the action of putting an object 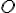 to the location
to the location 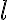 . Obviously, based on the above presumptions,
. Obviously, based on the above presumptions, 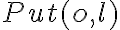 is only possible if
is only possible if 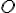 is movable and
is movable and 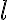 is not already occupied by another object. In addition, we have to consider that objects in drawers are not accessible unless the the drawer is open. We can capture this knowledge in a fluent accessible and a possibility axiom,
is not already occupied by another object. In addition, we have to consider that objects in drawers are not accessible unless the the drawer is open. We can capture this knowledge in a fluent accessible and a possibility axiom,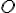 to hold in situation
to hold in situation  ,
, 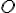 's location must either not be a drawer, or, if it is a drawer, it must be open. Otherwise, the object is not accessible. The positive effect of
's location must either not be a drawer, or, if it is a drawer, it must be open. Otherwise, the object is not accessible. The positive effect of 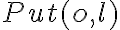 is that the object will be at location
is that the object will be at location 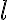 in the successor state, whereas the negative effect is that it will disappear from its original location:
in the successor state, whereas the negative effect is that it will disappear from its original location:2.3. Inferring a popcorn making plan
In this section, we introduce an axiomatization of the popcorn world, which allows us to derive a sequence of actions that achieves a subgoal of the popcorn making plan. We leave the specification of remaining axioms as an exercise to the reader. Let us consider the action sequence
- Put(Pot01, StoveCenter),
- Pour(Bowl01, Pot01),
- TurnKnob(switch(StoveCenter)),
- Wait(3),
- Put(Plate01, TableTopLeft),
- Pour(Pot01, Plate01).
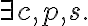 type(c, Corn)
type(c, Corn)  popped(c, s)
popped(c, s)  type(p, Plate)
type(p, Plate) 
In the previous section, we already provided a model of the Put action, which we can reuse so we move on and create a model of Pouring. The Pour(f,t) action denotes the transfer of a substance contained from a source container
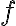 to a destination container
to a destination container 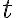 . For simplicity, we will assume here that any container can hold exactly one unit of volume, and that Pour will cause a complete transfer, i.e., there will not be any leftovers in the source container after pouring. As preconditions, we require the destination container to be empty and unobstructed. Unobstructed means that the container is not covered by anything (like a lid), and that there is sufficient free space above its opening such that the pouring can be performed. Obviously, in our popcorn world, a container is only unobstructed if it is located at one of the counter tops or the stove, and there is nothing on top of it, i.e.,
. For simplicity, we will assume here that any container can hold exactly one unit of volume, and that Pour will cause a complete transfer, i.e., there will not be any leftovers in the source container after pouring. As preconditions, we require the destination container to be empty and unobstructed. Unobstructed means that the container is not covered by anything (like a lid), and that there is sufficient free space above its opening such that the pouring can be performed. Obviously, in our popcorn world, a container is only unobstructed if it is located at one of the counter tops or the stove, and there is nothing on top of it, i.e.,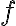 and
and 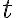 must be containers,
must be containers, 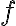 must be non-empty and accessible, and
must be non-empty and accessible, and 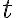 must be empty and unobstructed. As postconditions, Pour will cause the contents of the source container to be in the destination container, whereas it ceases being in the source container:
must be empty and unobstructed. As postconditions, Pour will cause the contents of the source container to be in the destination container, whereas it ceases being in the source container:The core functionality of a switch is to toggle the state of an electrical device
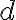 in a situation
in a situation  between switchedOn and
between switchedOn and 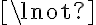 switchedOn. We introduce a TurnKnob(k) action, which operates on a knob and flips an electrical device's state. It is possible to execute TurnKnob(k) if
switchedOn. We introduce a TurnKnob(k) action, which operates on a knob and flips an electrical device's state. It is possible to execute TurnKnob(k) if 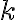 is a knob and belongs to an electrical device:
is a knob and belongs to an electrical device: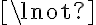 switchedOn(d,s) to switchedOn(d, do(TurnKnob(k),s)), and back:
switchedOn(d,s) to switchedOn(d, do(TurnKnob(k),s)), and back:The final missing step in our world model is the popping process of the corn. In order for the corn to pop, it must be exposed to heat for 3 minutes. In a real-world setting, it would be desirable if a robot agent were able to spend the time until the corn has popped more useful, but for now we assume that it bridges this idle time with waiting. To this end, we introduce an action Wait(t), during which the agent sleeps for the given amount of time. First, let us specify that it is always possible to wait and do nothing:
Starting from the initial state, it can be proven that our goal state in Equation can be reached by the action sequence
2.4. Complexity of logical reasoning
Representing models of the world and actions in situation calculus using FOL is extremely powerful and expressive, but comes with practical limitations. The perhaps most severe limitation affects the computational complexity of reasoning. Reasoning in logic denotes the automated verification of sentences given the facts and rules about the world. As an example, consider a rule, such as
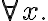 type(x, Bowl)
type(x, Bowl) 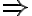 type(x, Container),
type(x, Container),
as part of a taxonomic relation stating that every object of the type bowl also is of the type container, and the fact type(Bowl01, Bowl) that assigns the entity Bowl01 the type Bowl. In order to prove that type(Bowl01, Container) also holds, we have to find a substitution of 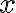 in the equation, such that the formula gets satisfied by its atomic constituents. This is the case for the substitution [x/Bowl01], as
in the equation, such that the formula gets satisfied by its atomic constituents. This is the case for the substitution [x/Bowl01], as
(type(x, Bowl) 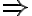 type(x, Container))[x/Bowl01]
type(x, Container))[x/Bowl01] type(Bowl01, Bowl)
type(Bowl01, Bowl) 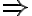 type(Bowl01, Container)
type(Bowl01, Container)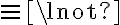 type(Bowl01, Bowl)
type(Bowl01, Bowl) 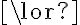 type(Bowl01, Container),
type(Bowl01, Container),
which is satisified if and only if type(Bowl01, Container) holds. The reasoning problem in FOL can thus be phrased as a search problem in the space of possible variable substitutions, which is called the Herbrandt universe. The elimination of variables by substitution through constant or function symbols is also called grounding or propositionalization, as a sentence whose variables have been substituted corresponds to an expression in propositional logic. However, the problem of finding a truth assignment satisfying a sentence in PL has been proven NP complete (Cook, 1971), so the computational expense of reasoning does scale exponentially in the number ground atoms. In addition, the Herbrandt universe typically is infinite as it contains both constant symbols and functions. As a consequence, it is not guaranteed that a search algorithm will terminate in all cases. It can be shown that every proposition that is entailed by a knowledge base in FOL can be deduced from a finite subset of the Herbrandt universe, whereas no method exists that is capable of proving non-entailment for all propositions that are not entailed by the knowledge base. This makes the reasoning problem in FOL semi-decidable (Turing, 1936; Church, 1936a; Church, 1936b). This means that for reasoning tasks that robots have to do it often pays off to limit the expressiveness of the representation language to what is needed and to think about whether the inference tasks can also be accomplished by more specific algorithms that can exploit the problem structure. Fast reasoning is particularly important for robot agents that are to act efficiently as in many cases the robot can start acting only after the reasoning tasks are completed.
2.5. Implementation of planning systems
Due to the undecidability of FOL, pratical implementations of KR&R systems use subsets FOL that make reasoning feasible. We will in the following briefly depict the most prominent action planning systems for robot agents.
In principle, there are two possible ways of solving a planning problem, namely progression planning and regression planning. Progression planning starts with the initial situation 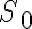 and builds up a state space graph as described in \ref{sec:evolution-modelling} by applying action sequences to
and builds up a state space graph as described in \ref{sec:evolution-modelling} by applying action sequences to  and monitoring the progress of the model, until a sequence is found that produces a final situation satisfying the goal specification. In contrast, regression planning starts with the goal specification, and searches backwards an action sequence whose first action is applicable in
and monitoring the progress of the model, until a sequence is found that produces a final situation satisfying the goal specification. In contrast, regression planning starts with the goal specification, and searches backwards an action sequence whose first action is applicable in  . In many cases, regression planning is computationally more efficient than progression planning. The most important reason for this is that in regression planning, only the relevant actions need to be considered, i.e., actions whose effects make the goal specification effectively true, whereas in progression planning, all applicable actions have to be considered.
. In many cases, regression planning is computationally more efficient than progression planning. The most important reason for this is that in regression planning, only the relevant actions need to be considered, i.e., actions whose effects make the goal specification effectively true, whereas in progression planning, all applicable actions have to be considered.
STRIPS. One of the first and best-known frameworks for formulating and solving planning problems is the STanford Research Institute Problem Solver (STRIPS) by Fikes, 1971. In essence, STRIPS is based on situation calculus but uses a restricted terminology to formulate rules. In STRIPS, action pre- and postconditions and goal specifications are required to be conjunctions of function-free literals. A literal is an atomic expression, which may also be negated. Action postconditions are also required to be function-free literals. By disallowing function symbols, the Herbrandt universe in STRIPS is finite and thus decidability can be guaranteed. In addition, STRIPS does not produce copies of all axioms in every situation, but maintains a single world representation that is modified by the reasoning procedures. The state representation only consists of positive literals. All literals not explicitly mentioned are assumed to be false (closed-world assumption). Negative effects of actions cause the respective literals to be deleted from the world state, positive effects are added to it. Action effects are thus typically divided into an addition and a deletion list. A plan in STRIPS is an action sequence that, when being executed in the initial state, leads to a state that satisfies the goal.
PDDL. The Planning domain definition language (PDDL) developed by Ghallab, 1998. Like in STRIPS, actions are defined by their preconditions and effects. However, these conditions are allowed to take not only the form of conjunctions of literals, but also universally and existentially quantified variables and implications are allowed. PDDL is based on a typed logic, i.e., variables may have domain constraints, which can simplify knowledge engineering enormously since most entities in the real world can be assigned some sort of category. A very powerful feature of PDDL is the concept of hierarchical action descriptions, which allows to model activities that are composed of multiple simpler actions. These subactions can be specified to be executed in a series or in parallel. For example, in a table-setting scenario, the order in which items are brought to the table is irrelevant, whereas in a recipe, the steps must be executed one after another. The result in such cases is called a partially-ordered plan. PDDL has been designed as a language unifying many features of planning systems at the time of its inception with the goal of fostering comparability, reuse and exchange of models. It has since then evolved to a quasi-standard that is used in many international planning competitions.
2.6. Discussing logic-based planning of popcorn making
The logic-based approach to reasoning about the actions of a robot agent has several attractive advantages over other forms of robot decision making. Given a model formalized as a set of logical axioms, which correctly and completely represents a robot, its actions, and the environment in some model, a robot agent can compute action plans for every goal that it is able to accomplish (Kowalski, 1979). Further, every action plan that the robot agent computes this way is guaranteed to be correct with respect to the formalized model. The set of axioms represents the knowledge about actions, their preconditions, and effects in a very modular, transparent, and explicit way. For every deduced action plan the robot agent can use the proof for the plan existence as an explanation of how the derived plan can achieve the goal. Finally, the competence of the robot agent can be incrementally increased by stating additional axioms formalizing new objects, actions, and environment conditions.
These advantages motivated many researchers to pursue a logic-based approach to reasoning about action. The logical approach to reasoning about action is presented in several textbooks, most notably in the ones by Reiter, 2001; Genesereth 1987; Davis, 1990, and Mueller, 2006. Seminal research papers promoting the logical approach to reasoning about action include McCarthy, 1969; McCarthy, 1968; Hayes, 1977; Hayes, 1979; Hayes, 1985. There have also been attempts to standardize knowledge representation and reasoning, as for example, in the Knowledge Interchange Format (Genesereth, 1998).
One caveat about the logical approach is that its advantages can only be leveraged if the respective robots, environment, and actions can be faithfully formalized as a consistent set of axioms. How to come up with sets of axioms that are consistent, logically entail all intended conclusions, and forbid unwanted ones is often a difficult knowledge engineering and research activity.
The research work on knowledge-based reasoning about actions is much too extensive to be covered in a book chapter. Therefore, in the remainder of this section we sketch relevant extensions to the logic based reasoning approach and refer to textbooks and seminal papers for more thorough and deeper accounts of the respective research topics.
When trying to come up with the appropriate logic-based axiomatizations for reasoning about robot actions one often experiences a lack of expressiveness and limitations of the state transition system model with atomic state transitions. In response to these limitations, various extensions have been proposed to deal with parallel actions (Baral, 1997), temporal aspects of action execution (McDermott, 1982; Allen, 1983; McDermott, 1985}, resource consumption through actions (Dean, 1991; Dechter, 2003}, and other shortcomings of the original approach.
Another limitation that is particularly critical for the control of robot agents is the inability of dealing with nondeterministic and probabilistic aspects of actions (Fagin, 1990). To respond to these limitations researchers have investigated non-montonic (McCarthy, 1980; McCarthy, 1986}, probabilistic (Hanks, 1990; Beetz, 2005) and decision-theoretic approaches (Boutilier, 1998; Haddawy, 1990; Haddawy, 1993; Kaelbling, 1998) to decide on the course of action that has the highest expected utility. In order to further increase the expressive power of the representation mechanisms researchers have also proposed approaches that can reason about the information preconditions of actions, such as knowing the combination before opening a safe (Moore, 1985; Morgenstern, 1987) and for representing not only the state of the environment but also an agent's beliefs with respect to the environment state (Bratman, 1988; Rao, 1991).
Some of the reasoning problems addressed are particularly relevant for autonomous robotics such as the indistinguishability of objects with respect to their perceptual features. Perhaps the best known is the "bomb into the toilet'' problem (McDermott, 1987), in which a robot looking at two identical packages is asked to disarm the bomb by putting it into the toilet. In this case, the proper plan is to put both packages into the toilet because it is the only way to ensure that the bomb is disarmed. This problem is closely related to the so-called symbol grounding problem (Harnad, 1990). The symbol grounding problem entails the problem that the semantics of logic languages assigns symbolic names objects in the real world as their meanings. This is critical because in many cases the perceptual apparatus of robots cannot effectively distinguish between different objects in question. One way of dealing with these problems is to extend the scope of reasoning also to the grounding of symbols. When setting the table the identity of a cup typically does not matter as long as the cup is clean and empty. When disarming a bomb, all candidate individuals should be disarmed in order to avoid an explosion. Only reasoning systems that can reason about the consequences of grounding symbols one way or the other can deal in informed ways with cases where the robot control system cannot properly ground a symbolic representation.
A heated debate about deduction being sufficient for realizing the common-sense capabilities of humans was triggered by the so-called Yale shooting problem (Hanks, 1987). The problems in solving the Yale shooting problem were taken by a number of researchers as an indication that a single logical reasoning mechanism might not be sufficient to solve both prospective and diagnostic reasoning tasks in reasoning about action (McDermott, 1987). One way of dealing with this issue is to employ multiple expert reasoners (Ferrucci, 2010), which, however, also yields the problem of how to deal with situations where different reasoners propose different solutions.
There have also been attempts to formalize more detailed and realistic models of manipulation actions in logic formalisms. This research agenda was originally been put forward in the two naive physics manifestos by Hayes, 1985; Hayes, 1985b). Perhaps the most insight providing activity was a challenge put forward by Davis and colleagues in which they asked for axiomatizing the task of cracking an egg and separating the egg yolk from the egg white (Miller: Common Sense Problem Page). The reasoning problem is that given an activity description of an egg cracking activity the reasoner has to answer an open collection of questions including: "What happens if: The cook brings the egg to impact very quickly? Very slowly? The cook lays the egg in the bowl and exerts steady pressure with his hand? The cook, having cracked the egg, attempts to peel it off its contents like a hard-boiled egg? The bowl is made of looseleaf paper? of soft clay? The bowl is smaller than the egg? The bowl is upside down? The cook tries this procedure with a hard-boiled egg? With a coconut? With an M&M?''} This exercise showed the dependence of the axiomatizations on the proper choice of abstractions and how quickly axiomatizations become overly complex as action models become more realistic (Morgenstern, 2001).
If we apply the knowledge representation and reasoning methods proposed in the previous section to the control of robot agents we see an important weakness of this approach. This weakness is that choosing the state transition system model with atomic state transitions as a model we make the assumption that the effects of actions are independent of the movements that a robot executes. This contradicts the view of robotics as the field that studies how to move the body of the robot to accomplish tasks.
3. KR&R within perception-action loops
In order to extend the knowledge representation and reasoning techniques we have discussed so far to reason about how to execute actions we will now consider more realistic representations of perception-action loops. This approach takes the view that a computational model for controlling a robot agent accomplishing complex manipulation tasks has to explain how vague instructions such as "pour the popcorn onto the plate'' can be translated into the body movements that the robot has to generate. To infer such a body motion the robot the robot needs to infer that it has to grasp the pot by the handles, hold the pot horizontally, tilt the pot around the axis between the handles, remove the lid before pouring, and so on.
3.1. Linking representation to perception and motion
- proposing suitable representations of motions that enable us to combine knowledge representation and reasoning with control engineering, cognitive psychology, and robot learning;
- maintaining and acquiring environment and object representations that are detailed enough for object manipulation; and
- maintaining and updating the symbolic representations by the robot perception system.
Representation and reasoning about motions
Let
us first look at suitable representations for robot body motions and
their physical effects. To develop such representations we can take
inspiration of how humans accomplish their manipulation actions through
the learning, planning, and execution of body motions, which is
intensively investigated in a research field that Prinz, 2013 call
action science. Action science lies in the intersection of several
research disciplines including cognitive psychology, cognitive
neuroscience, and sport science. These research threads contribute to
the representation and reasoning about actions as they investigate more
detailed and realistic models of manipulation actions.For example, Flanagan, 2006 propose a widely used conceptual model for representing and reasoning about the motions that constitute human manipulation actions. This model is depicted in the previous chapter. In this model the body motions of manipulation actions are composed of motion phases. For example, fetching and placing an object is composed of a reaching, a lifting, a transport, and a release phase. Each of these motion phases has a motion goal. The goal of the reaching phase is that the object is grasped, of the lifting phase that the object is lifted off the supporting surface, of the transport phase that the object is at the destination, and of the releasing phase that the object has left the hand. The transitions between the motion phases are so-called force-dynamic events (Siskind, 2001). The force-dynamic events, which also cause distinctive perceptual events in the perceptual system of the robot agent are the contact of the hand with the objects, the hand feeling the gravity of the object, the collision of the object with the destination surface, and the hand losing the grip of the object. The individual motion phases also have knowledge preconditions. When starting the reaching motion the robot must have decided on the target pose, when starting the lifting motion the robot must have committed to a holding pose, and so on.
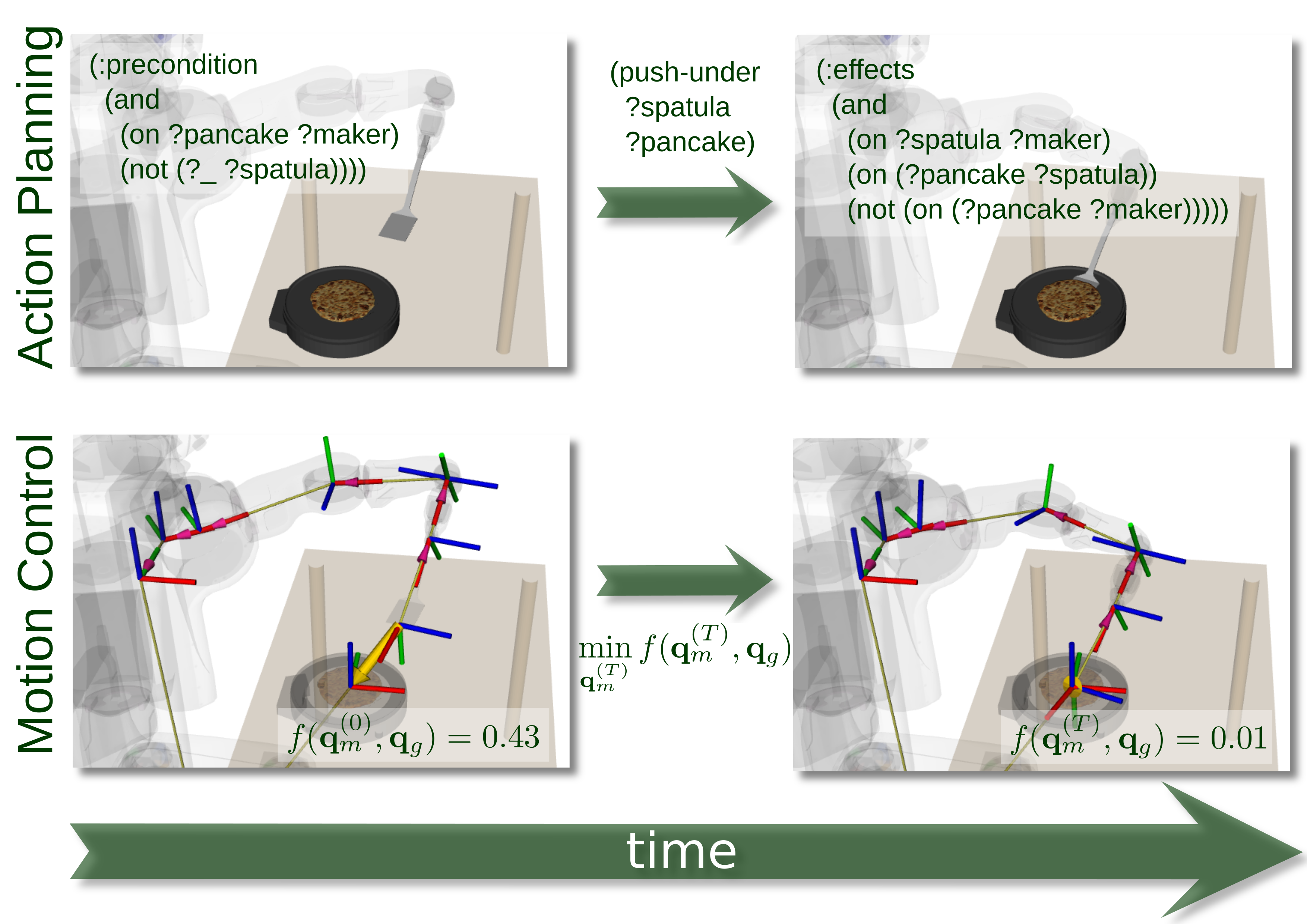
Fig. 1: Comparing the state transition system model with the constraint- and optimization-based control model of manipulation actions.
Another
approach to represent the manipulation actions at the motion level is
to represent the conceptual model underlying the constraint-and
optimization-based control frameworks (Khatib, 1987; Smits, 2009) In
constraint- and optimization-based control the bodies of robot agents
are represented as chains of control frames (6D poses of key conrol
points of the robot). Figure 1 compares
the state transition model with the constraint- and optimization-based
control model. While the logic approach represents the objects and
effects, the control approach specifies constraints and objectives on
motions. Therefore, the semantics of the manipulation actions, in
particular the causal relation between motion parameterization and their
physical effects, has to be encoded into the constraints and objectives
for the motions.
Knowledge-enabled robot programming
When
applying the Flannagan model the task of reasoning is to infer the
motion parameters for the individual motion phases and in constraint-
and optimization-based control the reasoning system has to infer the
motion constraints and objective functions to be optimized. This can be
accomplished through knowledge-enabled robot programming.
In the
knowledge-enabled programming style programmers equip robots with a
combination of generalized action plans and a knowledge base of general,
modular knowledge pieces. The basic idea of knowledge-enabled
programming is to separate knowledge from the control program and to
modularise it into small broadly applicable chunks, such as "grasp
objects by their handles'', "hold filled containers upright'', "do not
squeeze breakable items too hard'', etc. The program would ask: "How
should I pick up the object in front of me?''. A reasoning mechanism
would then collect the relevant knowledge units and combine them in
order to propose the appropriate grasp. The primary advantage is that
these knowledge pieces can be collected and that they can be reused by
other robots accomplishing different tasks with different objects in
different environments (Pratt, 2015). This reuse of generalized
knowledge can, therefore, drastically accelerate the realisation of new
robot applications. Figure~\ref{fig:generalized-knowledge} shows
examples of such generalized knowledge chunks, which can be conveniently
stated as logical axioms.
This idea of leveraging generalized plans for manipulation actions is also supported by a number of cognitive scientists including Schmidt (Drescher, 1991) suggest that movements within a class, such as fetch and place and pouring, share the same order of sub-movements and their relative timing. If these programs are to be executed in different contexts they are called generalized motion programs (or motion schemata) and include variable parameters (e.g., coordinates, body poses, timing, forces) are to be specified to the program. The parameterizations define the details of the movement and how it is executed for particular objects in particular contexts for different purposes. These generalized motion programs are called generalized motion plans if they cannot only be executed but also reasoned about and modified at execution time.

Fig. 2: A generalized motion plan for a pouring action.
Figure
2 show a generalized motion plan for pouring
actions. The plan consists of the signature of the plan and the body of
the plan. The signature includes the name of the plan, which is pour and the formal parameters names theme, source, and dest specifying
the destination of the theme to be poured out of the source container.
The formal parameters are typed: the theme is some substance, the source
is a container object that contains the theme, and the destination is a
location.
The power and
elegance of knowledge-enabled programming comes from facilitating the
application and combination of relevant knowledge pieces for specific
manipulation tasks. This enables robot agents to accomplish manipulation
tasks in new contexts much more competently, flexibly, and robustly.
(Note: As Pratt, 2015 puts it: "Robots are already making large
strides in their abilities, but as the generalisable knowledge
representation problem is addressed, the growth of robot capabilities
will begin in earnest, and it will likely be explosive. The effects on
economic output and human workers are certain to be profound.'')
Consider
again the task of picking up an object. Instead of implementing the
knowledge of how to pick up an object as a piece of code tailored for
the respective context the knowledge of how to pick up objects is
decomposed into a collection of generalized knowledge pieces as listed
in Figure \ref{fig:generalized-knowledge}. This way the knowledge pieces
can be applied to different robots, objects to be picked up, the tasks
for which the object are to be picked up, and the scenes in which the
objects are to be picked up.

(perform
The action description is vague or underdetermined because many pouring behaviors are possible executions of the action description. In Figure \ref{fig:making-popcorn} we have already seen two of them: the one-handed pouring of the popcorn from the bowl into the pot (upper row right) and the pouring of the popcorn from the pot onto the plate. Thus, in order to transform the underdetermined action description into a motion specification that can be executed by the generalized motion plan, the robot agent has to make a number of reasoned decisons based on current context possibly at planning or execution time. Examples of such decisions are which popcorn is meant and how much? The robot also has to choose a plate that is unused, clean, and has enough capacity.
robot has to infer the key movement constraints that ensure that the pot will not fall down, the popcorn on the plate and not spilled on the table including to hold the pot with two hands by its handles and
horizontally, to tilt the pot holding it in the right height and centered above the plate, and so on.
flexibility has to be paid for with the requirement of broader and deeper understanding of intuitive physics and the ability to regress effects into the motions that can achieve them.
3.2. Reasoning for object manipulation
We have just seen the kinds of refinements of action descriptions that make the context-specific execution of underdetermined action descriptions possible. So, let us now look at the knowledge representation and reasoning that can inform these refinements. The situation calculus representation we have discussed in the previous section cannot provide the necessary reasoning because of its use of action models that assert that actions cause the effects specified in the models if the preconditions of the actions are satisfied, which is only valid if the effects are independent of how actions are executed.
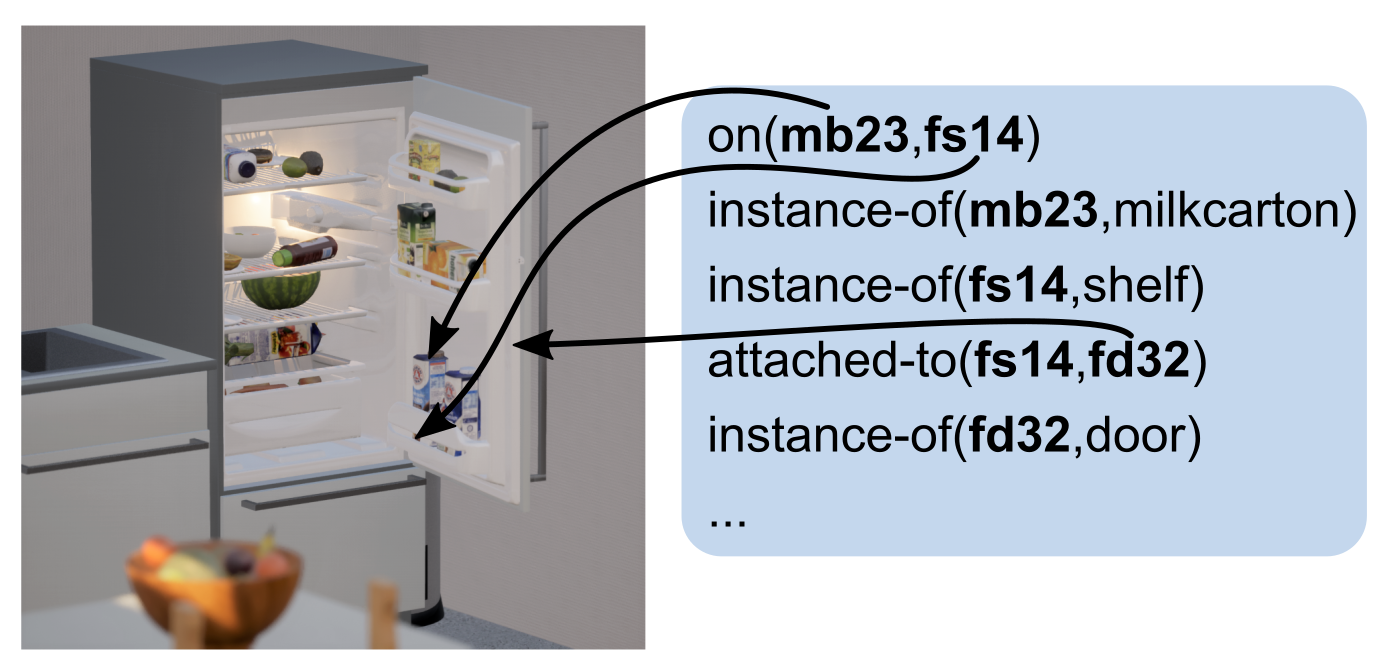
Fig. 1: Typical representation of a scene inside a refrigerator using predicate logic.
When robots execute actions the physical effects of the actions depend on how the actions are executed and what the specific action context is. In recent years more detailed representations of objects, environments, robots, and tasks have gained a lot of momentum. Reasons are advances in in representation learning in deep networks, which allow the automated learning of task-specific representations, and the ones in simulating and rendering virtual reality environments for computer games and other applications.
In this section we will look at the combination of logic representations with the ones used by simulation and rendering engines to enable robot agents to reason about how to move their bodies to accomplish underdetermined action descriptions. To do so, we will look at the problem of picking up a milk box from the refrigerator.
In predicate logic we can represent state of affairs such as entity mb23 is a milkbox located on a shelf that is attached to the door of the fridge. This state of affairs is depicted in Figure 1. If we want to represent the scene in more detail including the structure, the geometry, the appearance, the content, the physical properties, and the articulation of the objects in the environment the knowledge base becomes huge and difficult to reason with.
Representations with the necessary levels of detail have been successfully developed in modern virtual reality technology, in which huge realistic environments are represented very comprehensively and very detailed and physically simulated and rendered in real time and with currently available computing power. For example, already in 2015 the Unreal game engine showed the technology demonstration "a boy and his kite'', which featured realistic physics-based rendering of a 100 square miles environment with 15 million pieces of vegetation, realistically moving animals, and physics-enabled animation of a kite flying in changing wind conditions in real time at 30fps.
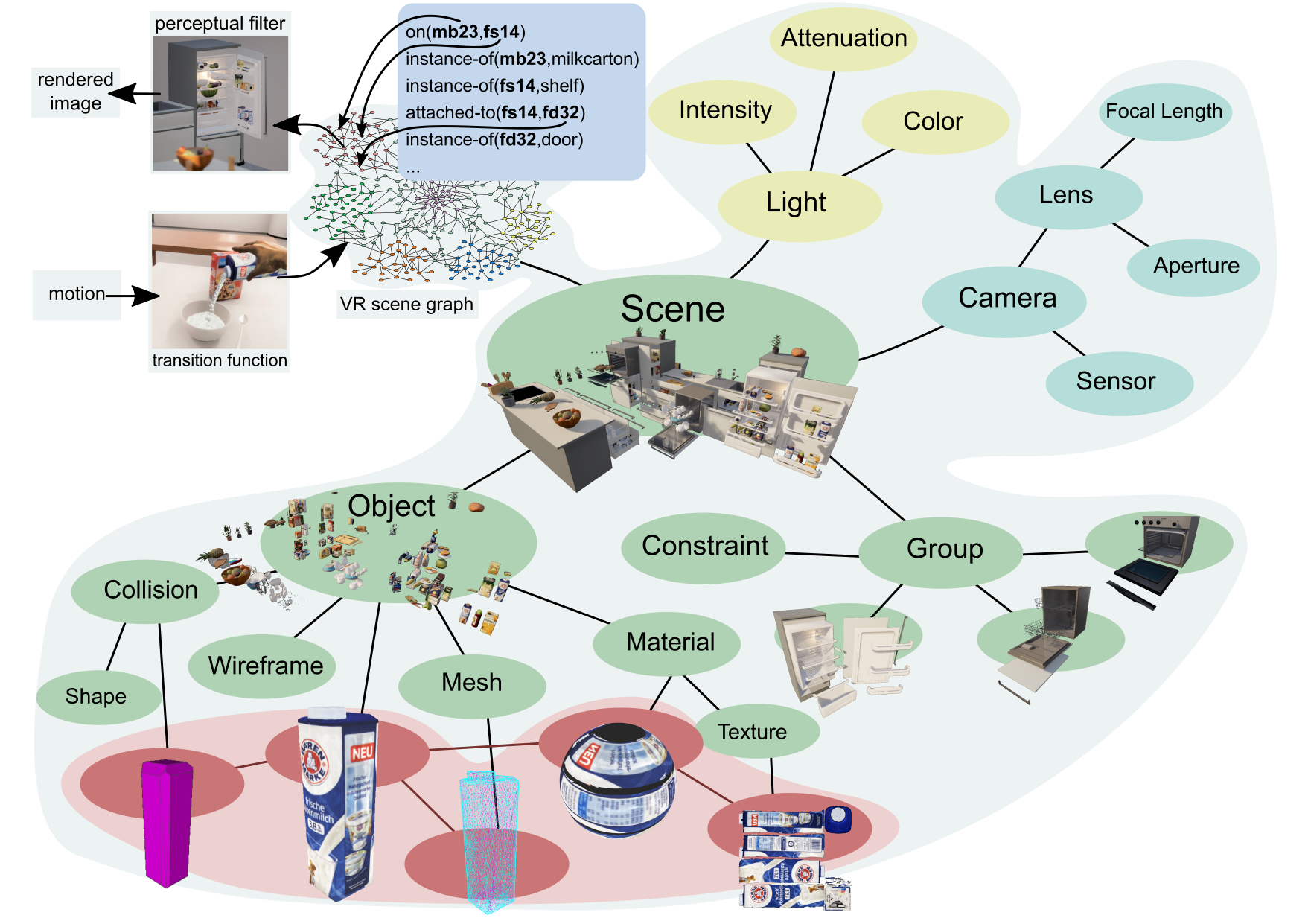
Fig. 2: Linking symbolic names of entities to nodes in scene graphs that represent these entities. The subtrees of the nodes contain the detailed representations of entities that are needed to infer context-specific paratmeterizations of actions.
Virtual reality systems represent environments as scene graphs, that are specifically designed data structures that contain all the information needed to render images and animations of 3D scenes. The scene graph is a tree-like data structure where the nodes represent subscenes and the child relations from a node p to the nodes 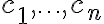 state that the scene p contains all subscenes
state that the scene p contains all subscenes 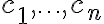 . The leaf nodes, called shape nodes, represent the geometry, appearance, lighting, texture, surface attributes, and material of the respective physical entity. The bodies of the entities are typically CAD models or meshes. The inner nodes hold a group or composition of children nodes that might be constrained by physical relations such as attachment, support, and articulation. Also children nodes might represent the subscene at different levels of detail based on distance to viewer. Or, they might represent different states of of a subscene like a container being open or closed. For rendering purposes the inner nodes might also contain light sources and local cameras. The inner nodes also include transformations that move, rotate, and scale the subscenes within its own reference frame.
. The leaf nodes, called shape nodes, represent the geometry, appearance, lighting, texture, surface attributes, and material of the respective physical entity. The bodies of the entities are typically CAD models or meshes. The inner nodes hold a group or composition of children nodes that might be constrained by physical relations such as attachment, support, and articulation. Also children nodes might represent the subscene at different levels of detail based on distance to viewer. Or, they might represent different states of of a subscene like a container being open or closed. For rendering purposes the inner nodes might also contain light sources and local cameras. The inner nodes also include transformations that move, rotate, and scale the subscenes within its own reference frame.
Scene graphs are highly optimized and facilitated by very fast and efficient algorithms for storing, managing very complex and detailed scenes, for retrieving information from them, for visual rendering them and simulating the physical effects of actions performed in the scenes.
Using scene graphs, we can realize detailed and multi resolution representations by linking symbolic entity names to the nodes in the scene graphs they represent, as it is shown in Figure 2. This way the KR&R system can make the detailed information available that is needed for the contextualization such as the geometry of the milk box, its parts, and its visual appearance. In the scene graph the milkbox is implemented as a subtree that contains all the data and computation mechanisms needed to realistically render and simulate the milkbox. This level of detail is sufficient for inferring body motions.
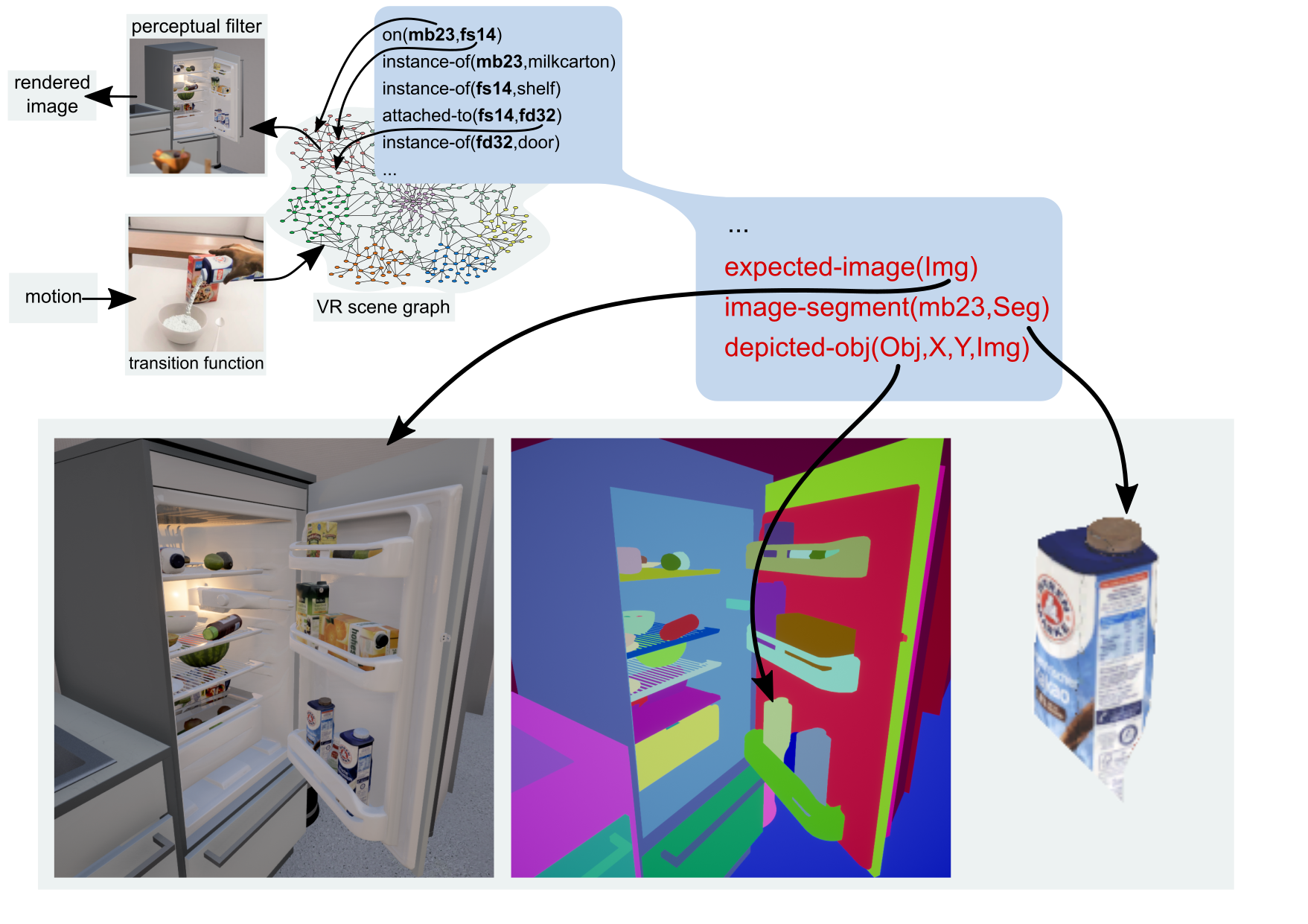
Fig. 3: Defining new predicates by computing their truth values through retrieving information from scene graphs and using the rendering process of the virtual reality environment.
Using the scene graphs, we can realize virtual knowledge bases using symbolic predicates that compute their truth values through procedural attachments. As shown for example in Figure 3, we can define a predicate expected-camera-image(Img), which is true for the image Img that the robot expects to see given its belief state. When the KR\&R reasoner tests the truth value of the statement expected-camera-image(Img) it represents the beliefs of the robot as a scene graph, creates a virtual camera that matches the technical specification of its own camera, places the camera acording its pose estimates, renders an image, and binds the image to the symbolic variable Img. A predicate image-segment(Obj,Segs,Img) relates each object Obj in an image Img with the image segments Segs depicting it by asserting that all other objects are invisible. Thus, using the detailed representations of scene graphs and the rendering and simulation capabilities of virtual reality engines the reasoning capabilities of KR&R frameworks can be substantially improved.
4. Conclusion
Knowledge representation and reasoning provides both, huge opportunities for the investigation of intelligent robots as well as huge challenges for KR&R research. The opportunities are well stated by Pratt, 2015: "Robots are already making large strides in their abilities, but as the generalizable knowledge representation problem is addressed, the growth of robot capabilities will begin in earnest, and it will likely be explosive.'' The challenges become obvious if we look at research in the field of action science. The brain has orchestrated very diverse, sophisticated, and powerful reasoning techniques to achieve the cognitive capability to accomplish complex goal-directed object manipulation capabilities. The representation and reasoning capabilities include simulation-based (Hesslow, 2002), probabilistic (Griffiths, 2008), imagistic (Kosslyn, 2005) reasoning, and prospection (Vernon, 2015). In addition, other information processing mechanisms including situation models that enable flexible, context-specific, goal-directed behavior as well as memory mechanisms (Tulving, 1972) are not understood well enough to build informative models of their operation. Other key research questions that deserve intensive research activities are how to ground reasoning techniques into the perception and action mechanisms of robot agents and how to combine symbolic representations with task-directed representations automatically generated through data intensive machine learning techniques.