Knowledge Representation & Reasoning: Logic-based knowledge representation

2. Logic-based knowledge representation and reasoning

2.1. Logic-based knowledge representation

We choose symbolic logic to formalize the entailment of conclusions from premises, in order to represent our model of popcorn making and robot agency in general. As shown in Figure 1, a logic formalism consists of three components: its syntax, its semantics, and its calculus:

the syntax determines what can be expressed by defining the set of symbol structures that constitute the logic language. The language is typically defined recursively through a set of atomic symbols and grammatical rules that define how symbolic expressions in the language can be combined to form more complex structures
the semantics determines what symbolic expressions mean by assigning the truth value to symbolic expression, where the semantics of atomic expressions is specified by an interpretation function and the semantics of a compound expression is computed from its constituents and the logical operator that connects the the constituents such as the "and,'' "or,'' and "negation'' operator.
the calculus that consists of symbolic expressions asserted to be true and rules for generating new symbol expressions from existing ones.

Components of a logic knowledge representation

Fig. 1: Components of a logic knowledge representation: syntax, semantics, and calculus.

If we use logic to encode problem-solving knowledge then the calculus of a logic can operate as a problem-solver. To this end, knowledge engineers have to carefully define the semantics of the atomic expressions. In addition, the the engineer has to assert a set of compound symbolic expressions as being true. The goal is to determine a compact set of expressions (an axiomatization) that together with the rules of the calculus creates only symbol structures that are entailed by the semantics, it is that the axiomatization is correct and that all symbolic expressions that are entailed can be generated by applying the calculus to the axiomatization, that is that the axiomatization is complete. Thus, if the knowledge engineer comes up with a correct and complete axiomatization of a problem domain, then a symbolic expression that represents some proposition in this domain is true if and only if it can be derived from the axiomatization using the calculus. This is important because this gives us an automatable computation process to test the truth of a symbolic expression.

Propositional logic. Let us consider propositional logic (PL) as our first example of a logic. In PL, every symbol is a Boolean proposition that can take the values true or false. A symbol thus is an atomic sentence, which cannot be further decomposed into finer-grained sentences. Two sentences may be connected by means of logical connectives 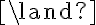$\land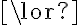$ ('and'), $\lor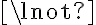$ ('or'), $\lnot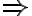$ ('not'), $\Rightarrow$ ('implies') and 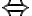$\Leftrightarrow$ ('equivalent') to form more complex sentences (in descending operator precedence). Brackets 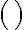$()$ may be used to accommodate precedence of connectives. In PL, we can represent the knowledge that the corn will pop when it is in the pot, the pot is located on the stove and the stove is switched on as follows:

corn-in-pot 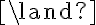$\land$ pot-on-stove 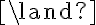$\land$ stove-switched-on 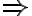$\Rightarrow$ corn-popped

The semantics of this representation of an implication is that, whenever we encounter the antecedant of both corn-in-pot, pot-on-stove, and stove-switched-on to be true, we can be sure that corn-popped will also be true. Starting from those three antecedant expressions, a calculus of PL should thus be able to derive corn-popped as a new expression.

PL is simple and intuitive, but at the same time limited in expressiveness and generality. What this means becomes evident if we try to apply the above representation to a kitchen with more than one stove tops, let us assume four. In order to represent the same knowledge, in the new environment we would need four sentences, one for every stove top, i.e.

corn-in-pot 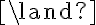$\land$ pot-on-stove1 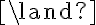$\land$ stove-1-switched-on 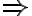$\Rightarrow$ corn-popped
corn-in-pot 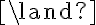$\land$ pot-on-stove2 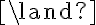$\land$ stove-2-switched-on 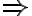$\Rightarrow$ corn-popped
corn-in-pot 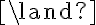$\land$ pot-on-stove3 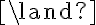$\land$ stove-3-switched-on 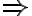$\Rightarrow$ corn-popped
corn-in-pot 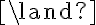$\land$ pot-on-stove4 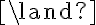$\land$ stove-4-switched-on 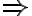$\Rightarrow$ corn-popped

Especially in large and complex environments, the representation of knowledge in PL can thus become unwieldy and cumbersome.

First-order logic. First-order logic (FOL, sometimes also first-order predicate logic, FOPL) is a generalization of PL that allows more complex and more expressive sentences than PL does. Unlike in PL, the representational symbols in FOL stand for single individual entities in the real world. Thus in FOL, a symbol alone is not a well-formed expression. Symbols may identify instances of real physical objects in the world, such as CookingPot-03 or Corn-0815, but may also refer to abstract things like

$42$ , Kilogram, or X. Propositions are made by means of predicates that are used to establish certain relations between symbols. For example, a binary in predicate can be used to establish a relation between the symbols for the corn and the cooking pot:

in(Corn-0815, CookingPot-03).

This statement is a well-formed FOL expression and can be interpreted as Boolean proposition that is either true or false: either the corn is located in the pot or it is not. An expression that consists of a single predicate symbol and a list of representational symbols is called a ground atom. Representational symbols are also called constant symbols.

Like in PL, expressions in FOL may be combined using the logical
connectives to form more complex expressions, such as

in(Corn-0815, CookingPot-03)

$\land\$ on(CookingPot-03,Stove-01)

$\land\$ switched_on(Stove-01)

$\Rightarrow$ popped(Corn-0815).

FOL has variables, which act as placeholders for representational symbols in a sentence. Variables help to formulate sentences about some or even all things in the universe. FOL is therefore suitable for representing universal knowledge and rules very compactly. Quantifying operators may be used to express restrictions on the number of possible variable substitutions for which the sentence must be true. There are two quantifiers, namely a universal and an existential quantifier. A sentence

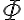$\Phi$ containing a universally quantified variable

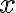$x$ is written as

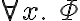$\forall x.\ \Phi$ , (literally "for all x'') and a sentence

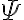$\Psi$ containing an existentially quantified variable is written

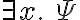$\exists x.\ \Psi$ (literally, "there exists x''). Consequently, using the universal quantifier

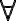$\forall$ , we can represent the knowledge that in general, corn pops when it is put in a cooking pot, which is located on a stove and the stove is turned on:

$\forall$ x,y,z. type(x,Corn)

$\land$ type(y,CookingPot)

$\land$ type(z,Stove)

$\land$ in(x, y)

$\land$ on(y,z)

$\land$ switched_on(z)

$\Rightarrow$ popped(x),

where we have introduced an additional relation type, which assigns an object category to every physical entity in the universe. This is necessary, as in standard FOL, the domain of every variable symbol ranges over all constant symbols and the state of being `popped' is only sensible for objects of the type 'corn'. Variables in a FOL sentence can be bound to a specific constant symbol by replacing every occurrence of the variable in the sentence by the respective symbol. We call the act of assigning a variable a symbol a substitution. To indicate that a variable

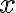$x$ is being substituted by the symbol

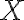$X$ in a sentence

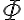$\Phi$ , we write

$\Phi[x/X]$ .

Predicates can be used to attribute certain properties to entities in the world. The type predicate, for instance, is binary and refers to the property of being of a certain type, like being a Stove or a CookingPot. Note that in this case, CookingPot, Corn and Stove do not represent instances of objects in the world but rather abstract type determiners. Object instances are represented by the constant symbols replacing the first argument of type. The predicates switched_on and popped are unary and attribute internal states to objects, namely the 'switched on' state and the 'having popped' state. on and in are binary, i.e., they establish a relation between pairs of entities. The predicates and constant symbols can thus be used to formulate facts about the state in which a robot agent believes the environment to be.

Besides constant and predicate symbols, a third kind of symbols are functions. The term 'function', in context of FOL, however, does not refer to a kind of sub-routine that takes arguments and returns a value. It is rather to be understood as an elegant way of referring to related things without the need of introducting a symbol for them. For example, we naturally talk about "the location of the corn'' without explicitly mentioning what the actual location is. The label "location of the corn'' always refers to the correct thing, even if we do not know what it is. Functions in FOL give us the same flexibility in computational knowledge representation. The function

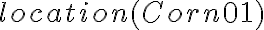$location(Corn01)$ , for instance, is a way of denoting the location of the corn in every possible state of the environment without knowing about its actual location. A function is a valid representational symbol itself, so functions can also be nested.

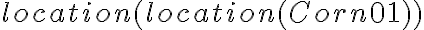$location(location(Corn01))$ , for example, denotes the location of the corn's location. As functions are representational terms, however, they are not valid sentences. Valid sentences about functions can be made through predicates, just like ordinary constant symbols, or by making their identity explicit using the equality operator '

$=$ '. At this point it is important to note that the semantics of a FOL is typically non-injective and non-surjective. This means that the mapping from symbols to objects in the real world is not necessarily complete and unambiguous, such that there may be objects that are not represented by any symbol, and there may be objects referred to by more than one symbol. The fact that two symbols refer to the identical object can be stated with the equality operator. In our running example, for instance,

location(location(Corn01)) = TableTopLeft

states that the location of the corn's location points to the same object as TableTopLeft. The nested location function can be regarded as a representational `shortcut' without the need to introduce a symbol for the location of the corn, if it is irrelevant in the expression, if the corn is located in the cooking pot or in the bowl, for instance. Functions in FOL are extremely powerful, but they also severely affect the computational complexity of reasoning, as we will discuss in greater detail.

FOL is a powerful formalism to describe real-world situations such as our popcorn world. However, the representations presented above describe rather static situations, `snapshots' of the kitchen counter taken at a particular time step. In the following, we will introduce a framework that brings dynamics into FOL representations and thus allows to manipulate and evolve the world over time.