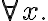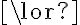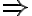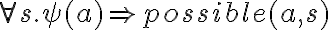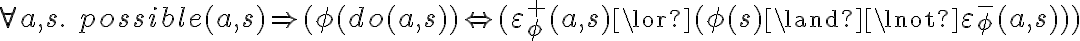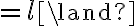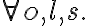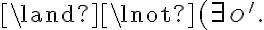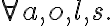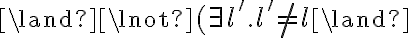Book
Knowledge Representation & Reasoning
Completion requirements
2. Logic-based knowledge representation and reasoning
2.2. Logic-based action planning
In order to model the evolution of the world over time, we describe a
framework in FOL called situation calculus. In situation calculus, world states and actions' pre- and postconditions are bound to an abstract symbol representing a certain situation. In context of a robot agent, a situation represents one cycle in the perception-action loop:
- Technically, a situation is denoted by a term in FOL, i.e., the constant symbol
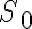 denoting the initial situation, or a function
denoting the initial situation, or a function 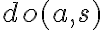 representing the situation that is obtained when an action
representing the situation that is obtained when an action  is executed in situation
is executed in situation  .
. - Actions are represented by terms in FOL. Constant symbols stand for actions without arguments (e.g., Stop), and functions represent actions that can be parameterized (e.g., Open(DrawerLeft)). There is a dedicated predicate
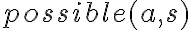 , which states that an action
, which states that an action  is applicable in situation
is applicable in situation  .
. - Fluents represent certain aspects of a world state that may change from one situation to another. Fluents can be represented by predicates, like
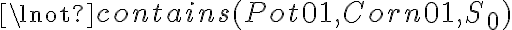 or functions like
or functions like 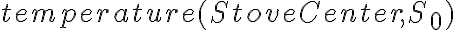 ). Fluents are always bound to specific situations that they refer to because they may change their values over time. States that are constant over all situations are called atemporary and do not need to be assigned a situation. Examples of such predicates are the \textit{type} assertions as introduced above, such as
). Fluents are always bound to specific situations that they refer to because they may change their values over time. States that are constant over all situations are called atemporary and do not need to be assigned a situation. Examples of such predicates are the \textit{type} assertions as introduced above, such as 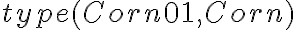 .
.
The function 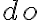 is also called projection as it predicts the states of future situations that are obtained through action execution. By nesting multiple do functions, one can represent the final situation that is obtained after execution of a complete sequence of actions. For example, the situation after execution of the three actions
is also called projection as it predicts the states of future situations that are obtained through action execution. By nesting multiple do functions, one can represent the final situation that is obtained after execution of a complete sequence of actions. For example, the situation after execution of the three actions
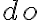 is also called projection as it predicts the states of future situations that are obtained through action execution. By nesting multiple do functions, one can represent the final situation that is obtained after execution of a complete sequence of actions. For example, the situation after execution of the three actions
is also called projection as it predicts the states of future situations that are obtained through action execution. By nesting multiple do functions, one can represent the final situation that is obtained after execution of a complete sequence of actions. For example, the situation after execution of the three actions- Put(Pot01, StoveCenter)
- Pour(Bowl01, Pot01)
- TurnKnow(switch(StoveCenter))
can be denoted by
do(TurnKnob(switch(StoveCenter)),
do(Pour(Bowl01, Pot01),
By convention, the last argument in the list of arguments (if any) always denotes the situation symbol.State Axioms. We have to describe the state of the environment in the initial situation 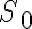 through fluent and atemporal axioms. In order to describe the popcorn world, for instance, we have to assert the types of objects in our environment:
through fluent and atemporal axioms. In order to describe the popcorn world, for instance, we have to assert the types of objects in our environment:
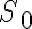 through fluent and atemporal axioms. In order to describe the popcorn world, for instance, we have to assert the types of objects in our environment:
through fluent and atemporal axioms. In order to describe the popcorn world, for instance, we have to assert the types of objects in our environment: type(ShelfLeft, Shelf)
type(ShelfLeft, Shelf)  type(ShelfRight, Shelf)
type(ShelfRight, Shelf) type(Corn01, Corn)
type(Corn01, Corn)  type(Pot01, CookingPot)
type(Pot01, CookingPot) type(Bowl01, Bowl)
type(Bowl01, Bowl)  type(Plate01, Plate)
type(Plate01, Plate)The atemporal axioms may also represent a subsumption relation in order to construct a hierarchy of concepts, e.g.,
which enables us to refer to collections of object types in later axioms. The fluents represent the mutable parts of a situation, such as the object locations:
...
Note that, in standard FOL, it is insufficient to only specify the positive axioms but we also need to declare what does not hold. It is, however, common to make a closed-world assumption, which means that the framework assumes all ground atoms to be false, whose truth values have not been explicitly declared.
Action axioms. Actions are represented by two kinds of axioms, the possibility axiom}, which specifies under which circumstances an action is possible, and a successor state axiom, which describes the way in which the successor situation is affected by an action. The possibility axioms are sentences in FOL of the form
Action axioms. Actions are represented by two kinds of axioms, the possibility axiom}, which specifies under which circumstances an action is possible, and a successor state axiom, which describes the way in which the successor situation is affected by an action. The possibility axioms are sentences in FOL of the form
where 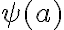 is a sentence with a free variable
is a sentence with a free variable  specifying the preconditions of the action
specifying the preconditions of the action  . The successor states are specified by axioms of the form
. The successor states are specified by axioms of the form
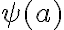 is a sentence with a free variable
is a sentence with a free variable  specifying the preconditions of the action
specifying the preconditions of the action 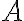 . The successor states are specified by axioms of the form
. The successor states are specified by axioms of the formwhere 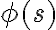 is a fluent declaration in situation
is a fluent declaration in situation  and
and 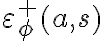 is a specification of the positive effects of an action
is a specification of the positive effects of an action  on
on 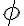 in situation
in situation  . Analogously,
. Analogously, 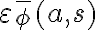 specifies the negative effects of action
specifies the negative effects of action  on
on 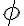 in
in  . An axiom of the form of the Equation can be read as follows: "In a situation
. An axiom of the form of the Equation can be read as follows: "In a situation  where action
where action  is applicable, the fluent
is applicable, the fluent 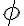 will hold after execution of
will hold after execution of  if and only if
if and only if  has made
has made 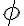 true (positive effect), or
true (positive effect), or 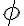 was already true in
was already true in  and
and  did not make
did not make 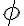 false (negative effect).''
false (negative effect).''
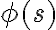 is a fluent declaration in situation
is a fluent declaration in situation  and
and 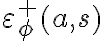 is a specification of the positive effects of an action
is a specification of the positive effects of an action  on
on 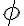 in situation
in situation  . Analogously,
. Analogously, 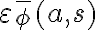 specifies the negative effects of action
specifies the negative effects of action  on
on 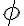 in
in  . An axiom of the form of the Equation can be read as follows: "In a situation
. An axiom of the form of the Equation can be read as follows: "In a situation  where action
where action  is applicable, the fluent
is applicable, the fluent 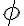 will hold after execution of
will hold after execution of  if and only if
if and only if  has made
has made 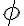 true (positive effect), or
true (positive effect), or 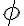 was already true in
was already true in  and
and  did not make
did not make 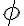 false (negative effect).''
false (negative effect).''The situations in situation calculus can be compared to single frames on a filmstrip, which is why these axioms are also called frame axioms. The action effects specifications determine the changes from one frame to the next one. However, only considering the aspects that
change is not enough. In most cases, only a small subset of fluents will be affected by an action and nearly all others stay the same. In FOL, this needs to be explicitly stated. In order to account for this problem, which is also known as the frame problem, it is necessary to also consider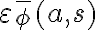 in the successor state axiom.
in the successor state axiom.
change is not enough. In most cases, only a small subset of fluents will be affected by an action and nearly all others stay the same. In FOL, this needs to be explicitly stated. In order to account for this problem, which is also known as the frame problem, it is necessary to also consider
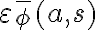 in the successor state axiom.
in the successor state axiom.As an exemplary action, we consider the action of moving an object from one location to another. In our popcorn world, we consider seven locations, at which movable objects may be put down, i.e., two counter tops, two shelves, two drawers and the stove top. For simplicity, we assume that each location is able to hold only one single object at a time. Let us first examine the possibility axiom for 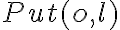 , which denotes the action of putting an object
, which denotes the action of putting an object 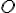 to the location
to the location 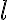 . Obviously, based on the above presumptions,
. Obviously, based on the above presumptions, 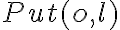 is only possible if
is only possible if 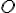 is movable and
is movable and 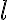 is not already occupied by another object. In addition, we have to consider that objects in drawers are not accessible unless the the drawer is open. We can capture this knowledge in a fluent accessible and a possibility axiom,
is not already occupied by another object. In addition, we have to consider that objects in drawers are not accessible unless the the drawer is open. We can capture this knowledge in a fluent accessible and a possibility axiom,
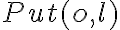 , which denotes the action of putting an object
, which denotes the action of putting an object 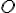 to the location
to the location 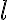 . Obviously, based on the above presumptions,
. Obviously, based on the above presumptions, 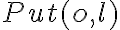 is only possible if
is only possible if 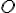 is movable and
is movable and 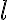 is not already occupied by another object. In addition, we have to consider that objects in drawers are not accessible unless the the drawer is open. We can capture this knowledge in a fluent accessible and a possibility axiom,
is not already occupied by another object. In addition, we have to consider that objects in drawers are not accessible unless the the drawer is open. We can capture this knowledge in a fluent accessible and a possibility axiom,For the accessible fluent of an object 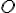 to hold in situation
to hold in situation  ,
, 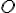 's location must either not be a drawer, or, if it is a drawer, it must be open. Otherwise, the object is not accessible. The positive effect of
's location must either not be a drawer, or, if it is a drawer, it must be open. Otherwise, the object is not accessible. The positive effect of 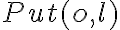 is that the object will be at location
is that the object will be at location 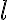 in the successor state, whereas the negative effect is that it will disappear from its original location:
in the successor state, whereas the negative effect is that it will disappear from its original location:
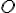 to hold in situation
to hold in situation  ,
, 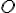 's location must either not be a drawer, or, if it is a drawer, it must be open. Otherwise, the object is not accessible. The positive effect of
's location must either not be a drawer, or, if it is a drawer, it must be open. Otherwise, the object is not accessible. The positive effect of 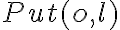 is that the object will be at location
is that the object will be at location 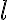 in the successor state, whereas the negative effect is that it will disappear from its original location:
in the successor state, whereas the negative effect is that it will disappear from its original location: